Cliquez sur l'une des cases suivantes :
|
|
|
|
|
CAPES externe 2012 |
|
|
Entraînement CAPES externe 2011 |
|
|
CAPES externe 2010 |
|
|
CAPES
externe 2009
|
|
|
ANALYSE
|
|
|
ALGEBRE/GEOMETRIE
|
|
|
ANALYSE
|
|
|
ALGEBRE/GEOMETRIE
|
|
|
SUJET 5
|
ANALYSE
|
|
SUJET 6
|
ALGEBRE
|
|
SUJET 7
|
GEOMETRIE
|
|
SUJET 8
|
ALGEBRE/GEOMETRIE
|
|
SUJET 9
|
ANALYSE
|
|
SUJET 10
|
ANALYSE
|
|
POUR
TELECHARGER L'ENSEMBLE DES 4 PREMIERS SUJETS AU FORMAT ZIP
|
Retour page d'accueil Coin des Matheux
EPREUVES ORALES
I) Dénombrements,probabilités,statistiques :
|
|
|
| Utilisation d'arbres,de tableaux,de diagrammes pour des exemples simples de dénombrement.Dénombrement des arrangements et des permutations. | Exemples simples de problèmes de dénombrement dans différentes situations. |
| Coefficients binomiaux,dénombrement des combinaisons,formule du binôme.Applications. | Exemples d'emploi de dénombrements pour le calcul de probabilités sur un ensemble fini d'épreuves,conformément aux programmes de Première. |
| Description mathématique d'une expérience aléatoire : ensemble des événements élémentaires,événements,probabilité( on se limitera au cas où l'ensemble d'événements élémentaires est fini.) | Exemples d'emploi de dénombrements pour le calcul de probabilités sur un ensemble fini d'épreuves,conformément aux programmes de Terminale. |
| Probabilité conditionnelle;indépendance de deux événements(on se limitera au cas où l'ensemble d'épreuves est fini).Applications à des calculs de probabilité. | Exemples de description et d'étude d'expériences aléatoires à l'aide d'une variable aléatoire. |
| Variable aléatoire à valeurs réelles dont l'ensemble des valeurs est fini.Loi de probabilité.Espérance mathématique,variance.Exemples. | Exemples d'expériences aléatoires et de calcul de probabilités attachées à ces expériences dans les cas de tirages avec ou sans remise.Exemples s'y ramenant. |
| Schéma de Bernoulli et loi binomiale.Exemples. | Exemples d'étude de situations faisant intervenir la notion de probabilité conditionnelle. |
| Séries statistiques à deux variables numériques.Nuage de points associé.Ajustement affine par la méthode des moindres carrés.Droites de regression.Applications.L'exposé pourra être illustré par un ou des exemples faisant appel à l'utilisation d'une calculatrice. | Exemples de situations tirées de la géométrie,des sciences appliquées ou de la vie courante amenant intuitivement aux notions de probabilité,de probabilité conditionnelle,d'espérance mathématique. |
| Exemples d'organisation et gestion de données statistiques au Collège | |
| Exemples d'organisation de données statistiques en classe de Seconde : Séries statistiques à une variable : regroupements en classes,effectifs,fréquences.Séries statistiques à une variable quantitative : effectifs cumulés,fréquences cumulées,caractéristiques de position et de dispersion(moyenne,écart-type). | |
| Exemples de traitement d'une série statistique à deux variables numériques.Etude du nuage de points associé : point moyen,corrélation linéaire,ajustement affine,droites de regression. | |
| Exemples de présentations de séries statistiques à deux variables en classe de Première ES.Présentation de l'information sous diverses formes : vocabulaire spécifique des tableaux;tableaux usuels;sous et sur-représentation. |
Retour
page d'accueil Coin des Matheux
II) Arithmétique :
|
|
|
Division euclidienne
dans 
, unicité du quotient et du reste.Applications. |
Exemples d'approches et d'applications du raisonnement par récurrence,dans des domaines variés,dans les classes de Première et de Terminale. |
Congruences dans
.Anneaux  |
Exemples de problèmes dont la résolution conduit à des calculs de PGCD ou PPCM de deux entiers naturels. |
| PGCD et PPCM de deux entiers naturels.Nombres premiers entre eux.Applications.L'exposé pourra être illustré par un ou des exemples faisant appel à l'usage d'une calculatrice. | Exemples de problèmes conduisant à la résolution d'équations du type : au+bv=k où a,b,k sont des entiers. |
| Nombres premiers;existence et unicité de la décomposition d'un nombre en facteurs premiers.Infinitude de l'ensemble des nombres premiers.Exple(s) d'algorithme(s) de recherche de nombres premiers.Usage de la calculatrice. | Exemples d'utilisation de la décomposition d'un entier naturel en produit de facteurs premiers. |
| L'anneau ;sous-groupes
additifs de .Les
idéaux de sont
principaux.Egalité de Bezout.Résolution dansd'une
equation de la forme ax+by = c |
|
| Nombres décimaux.Applications. | |
Construction du
corps  des
rationnels. |
Retour
page d'accueil Coin des Matheux
III) Nombres complexes :
|
|
|
Introduction et
construction du corps  des
complexes.Propriétés. |
Exemples d'emploi des nombres complexes dans des situations diverses issues des mathématiques,de la physique,... |
Définition
de ez pour z élément de .
Propriétés.Etude de la fonction de variable réelle
t
eit et,plus généralement,de
teat,où
a est élément de .Applications. |
Exemples d'emploi des nombres complexes pour l'étude de configurations en géométrie plane. |
| Racines n-ièmes d'un nombre complexe.Interprétation géométrique.Applications. | Exemples d'emploi des nombres complexes pour la recherche de lieux géométriques définis dans le plan par des conditions de distances et d'angles. |
| Module et argument d'un nombre complexe.Interprétation géométrique,lignes de niveau associées.Applications. | |
| Représentation
géométrique des nombres complexes.Interprétation
géométrique des applications : z z+b ,
z az et
z  où
a et b sont dans ,a
non-nul.Exemples d'application à l'étude de configurations
géométriques du plan. |
|
Etude de la transformation définie
dans le plan complexe par la fonction f : z
,où a et b sont complexes;lignes de niveau pour le module et l'argument
de f(z).Applications. |
Retour
page d'accueil Coin des Matheux
IV) Polynômes et systèmes :
|
|
|
| Fonction polynôme du second degré à coefficients réels.Mise sous forme canonique;application à l'étude du sens de variation et à la représentation graphique de la fonction.Equations et inéquations du second degré.On pourra utiliser la calculatrice. | Exemples d'étude,au niveau Collège,de problèmes conduisant à une équation ou une inéquation du premier degré. |
| Résolution des systèmes linéaires par opérations élémentaires sur les lignes.Méthode du pivot.Exemples. | Exemples d'étude,au niveau Collège,de problèmes conduisant à un système d'équations ou d'inéquations linéaires. |
| Exemples d'étude ,en Seconde et Première, de problèmes conduisant à une équation ou une inéquation du second degré. | |
| Exemples d'étude de situations conduisant à des régionnements de la droite ou du plan à partir d'inéquations du premier et du second degré. | |
| Exemples d'étude de situations conduisant à un système d'equations linéaires au niveau Lycée. | |
| Exemples d'étude,au niveau Lycée,de situations conduisant à un système d'inéquations linéaires.Applications simples aux problèmes de programmation linéaire à deux variables. | |
| Exemples de mise en oeuvre,en séances de T.P.,des principales compétences sur les pourcentages exigibles en Première ES. |
Retour
page d'accueil Coin des Matheux
V) Calcul vectoriel et méthodes analytiques :
|
|
|
| Caractérisation vectorielle d'une droite du plan.Représentations paramétriques.Génération des demi-droites,des segments.Parallélisme.Orthogonalité. | Exemples de présentation ,en Seconde,d'exercices
introduisant la notion de mesure d'un angle orienté de vecteurs
unitaires.Mesure principale.Cercle trigonométrique. Mise en évidence de l'intérêt de cette notion,à partir d'exemples d'utilisation dans le second cycle. |
| Equation cartésienne d'une droite du plan.Problèmes d'intersection,parallélisme.Condition pour que trois droites soient concourantes. | Exemples de présentation ,en fin de Collège,d'activités récapitulatives sur les calculs de longueurs et de distances dans le plan. |
| Equation cartésienne d'une droite du plan euclidien.Application à l'étude d'inéquations de la forme : acos t+bsin t >c | Exemples d'emploi du produit scalaire pour le calcul de distances,d'angles et d'aires dans les configurations usuelles du plan( triangles,polygones,...) |
| Définition et propriétés du produit scalaire dans le plan;expression dans une base orthonormale.Application au calcul de distances et d'angles. | Exemples d'emploi du produit scalaire et du produit vectoriel pour le calcul de distances,angles,aires,volumes,dans les configurations usuelles de l'espace(parallélépipède,tétraèdre,pyramide,... ) |
| Produit vectoriel dans l'espace euclidien orienté de dimension 3.Point de vue géométrique,point de vue analytique.Applications. | Exemples d'emploi des barycentres pour l'étude de configurations du plan et de l'espace ou la recherche de lieux géométriques. |
| Applications du produit scalaire et du produit vectoriel dans l'espace orienté : calculs de distances,d'aires,de volumes,d'angles... | Exemples d'emploi du produit scalaire pour la recherche de lieux géométriques dans le plan. |
Etude de l'application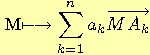 
.Définition et propriétés du barycentre de n points
pondérés.Associativité;application à la détermination
de barycentres attachés à des configurations usuelles du
plan,de l'espace. |
Exemples d'applications de différentes expressions du produit scalaire dans l'étude de configurations. |
| Droites et plans dans l'espace.Equations.Positions relatives;plans contenant une droite donnée. | |
| Orthogonalité dans l'espace affine euclidien : droites orthogonales,droite orthogonale à un plan,plans perpendiculaires.Applications. |
Retour
page d'accueil Coin des Matheux
VI) Configurations :
|
|
|
| Droites remarquables du triangle : bissectrices,hauteurs,médianes,médiatrices...(dans l'ordre que l'on voudra). | Exemples d'étude de configurations faisant l'objet de constructions géométriques à la règle et au compas. |
| Le cercle.Positions relatives d'une droite et d'un cercle,de deux cercles.Point de vue géométrique et point de vue analytique.Lien entre les deux points de vue. | Exemples de recherche et de représentations (perspective,vraie grandeur,...) de sections planes de solides usuels(tétraèdre,cube,pyramide,prisme,... ) |
| Théorème de l'angle inscrit : ensemble des points M du plan tels que l'angle orienté de droites ou de demi-droites(MA,MB) soit constant.Cocyclicité.Applications. | Exemples de présentation,au Lycée,de droites remarquables du tétraèdre : concours des médianes,condition concours des hauteurs;cas du tétraèdre régulier. |
| Relations métriques dans un triangle rectangle.Trigonométrie.Applications. | Exemples de problèmes d'alignement et de concours portant sur le triangle. |
| Relations métriques et trigonométriques dans un triangle quelconque.Applications. | Analyse comparée de différentes méthodes(calcul vectoriel,transformations,emploi d'un repère,nombres complexes,...) pour la recherche d'un même problème d'alignement ou d'orthogonalité dans le plan. |
| Exemples de construction de triangles satisfaisant à des conditions métriques ou géométriques imposées. | |
| Exemples de présentations de polygones réguliers usuels s'appuyant sur les méthodes du Collège(angles,rotations,...) et du Lycée(nombres complexes,... ) |
Retour
page d'accueil Coin des Matheux
VII) Projections,homothéties,translations,affinités :
|
|
|
| Théorème de Thalès.Projection dans le plan et dans l'espace,caractère affine des projections. | Exemples d'emploi,au niveau du lycée,de transformations pour l'étude de configurations du plan. |
| Homothéties et translations;transformation vectorielle associée.Invariants élémentaires : effet sur les directions,l'alignement,les distances...Applications à l'action sur les configurations usuelles. | Exemples d'emploi d'homothéties et de translations pour l'étude de problèmes d'alignement et de concours dans le plan. |
| Projection orthogonale sur une droite du
plan,projection vectorielle associée. Applications(calculs de distances et d'angles ,optimisation,...) |
Exemples d'emploi d'homothéties et de translations pour l'étude de problèmes de constructions géométriques dans le plan. |
| Ellipse déduite d'un cercle par affinité orthogonale dans le plan.Applications(en particulier,projection orthogonale d'un cercle sur un plan). | Exemples d'utilisation de la conservation du barycentre par certaines applications pour l'étude de configurations du plan ou de l'espace. |
| Composées d'homothéties et
de translations du plan.Relation vectorielle caractéristique. Groupe des homothéties-translations.Applications. |
Retour
page d'accueil Coin des Matheux
VIII) Isométries et similitudes :
|
|
|
| Réflexion du plan échangeant deux points donnés;médiatrice,régionnement associé.Applications au triangle et au cercle(cercle circonscrit,angle inscrit...). | Exemples de recherche et d'étude des isométries laissant invariante une configuration du plan. |
| Réflexions du plan échangeant deux droites sécantes données,bissectrices.Applications au triangle et au cercle(cercle inscrit ,tangentes à un cercle...). | Exemples de mise en oeuvre de différentes méthodes (composition de transformations,nombres complexes,...) pour la recherche des isométries ou des similitudes directes transformant une configuration usuelle donnée du plan en une autre(triangles,rectangles,...). |
| Recherche des isométries du plan conservant un carré,un losange,un parallélogramme,un rectangle(dans l'ordre que l'on voudra...) | Exemples d'emploi de composition et de décomposition d'isométries du plan pour l'étude d'une configuration. |
| Réflexions et rotations du plan.Invariants élémentaires : effet sur les distances,l'alignement,les angles.Application à l'action sur les configurations usuelles. | Exemples d'emploi de similitudes directes du plan pour l'étude d'une configuration. |
| Groupe des isométries du plan : décomposition d'une isométrie en produit de réflexions,groupe des déplacements,classification des isométries à partir de l'ensemble des points invariants. | |
| Composée d'une homothétie de rapport positif et d'une rotation de même centre;effet sur les distances,conservation des angles orientés.Similitudes directes.Ecriture complexe.Groupe des similitudes directes. | |
| Etude des transformations du plan euclidien qui conservent les rapports de distance. | |
| Recherche des isométries du plan conservant un polygone régulier;exemples(triangle équilatéral,carré,hexagone,octogone...) | |
| Réflexion de l'espace échangeant deux points donnés;plan médiateur,régionnement associé.Etude des isométries de l'espace ayant une droite de points invariants. | |
| Réflexions et rotations de l'espace.Invariants élémentaires : effet sur les distances,les angles...Applications à l'action sur les configurations usuelles. |
Retour
page d'accueil Coin des Matheux
IX) Courbes paramétrées,coniques :
|
|
|
| Courbes définies par des équations paramétriques dans le plan.Vecteur dérivé et tangente;interprétation cinématique. | Analyse comparée de différentes méthodes(calcul vectoriel,transformations,emploi d'un repère,nombres complexes,...) pour la recherche d'un même problème de lieu géométrique du plan. |
| Définitions de la parabole,géométriquement et par équation réduite;équivalence entre ces définitions.Construction de la tangente et de la normale en un point. | Exemples de présentation d'exercices sur les coniques(parabole,hyperbole,ellipse) au niveau du lycée. |
| Définitions de l'ellipse,géométriquement et par équation réduite;équivalence entre ces définitions. | Exemples d'étude de lieux géométriques à l'aide d'un paramétrage. |
| Définitions de l'hyperbole,géométriquement et par équation réduite;équivalence entre ces définitions. | Exemples d'étude de situations issues de la géométrie,de la mécanique ou de la physique conduisant à des courbes paramétrées. |
| Exemples de réprésentation paramétrique des coniques;constructions de la tangente et de la normale en un point à une parabole,à une ellipse, à une hyperbole. |