Définition de e^z pour z élément de  .Propriétés.Etude de la fonction de variable réelle te^it et,plus généralement, de te^at,où a est élément de .Applications.

Pré requis :

• identités remarquables
• nombres complexes
• fonctions trigonométriques
• exponentielle réelle
• définitions d'homomorphisme,d'application surjective,de sous-groupe

I) Définition de e^z , z :
 

1) Rappel et définition :

x , cos x + isin x = e^ix

x , cos x - isin x = e^-ix
 

Alors : x , cos x = ( e^ix + e^-ix ) / 2

sin x = ( e^ix - e^-ix) / 2i

Définition :

Soit z , z = a + ib , (a,b)²

e^z = e^{a + ib} = e^a( cos b + isin b )
 

Rque :

Si z  , e^z est l'exponentielle réelle .
 

Propriétés :

1) z , z'  , e^z+z' = e^ze^z'

2) z , e^z*

3) z, e^-z = (e^z )^-1

4) z ,   _e=

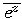
5) z , z = a + ib , (a,b) ²

| e^z | = e^a , Re(e^z) = e^acos b , Im(e^z) = e^asin b

arg(e^z) = b [2]
 

e^{z - z} = e⁰ = 1

Or ,d'après 1) , e^{z - z} = e^ze^-z

D'où , e^ze^-z = 1 , 1 élément neutre du groupe ( ^* , . )

Donc e^-z =( e^z )^-1

Propriétés :

6) z, e^z = 1  z  2i

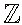
7) ( z,z' )² , e^z = e^z' z - z'  2i
 
 

II) Etude de la fonction de variable réelle t e^it :

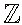
Notons  :  , t(t) = e^it = cos t + isin t
 

Propriété algébrique de  :

U = { z  , | z | = 1 }

(U , . ) est un sous-groupe de (^* , . )
 
 

Théorème :

est un homomorphisme surjectif de (  , + ) dans ( U , . )
 
 

Démo :

t , | (t) | = | e^it | = | e^{0 + it} | = e⁰ = 1

( t,t' ) ² , ( t+t' ) = e^{i( t+t' )} = e^ite^it' = (t)(t')

Si zU , z =cos  + isin  avec  =   ^{[ 2]}

dans R = 

M est l'image de z sur le cercle trigonométrique .

z = ()

Rque :

n'est pas injective

Ker  = { t  , (t) = 1 }

On a (t) = 1  e^it = 1

t  2

Donc :

Ker  = 2

Rque :

Premier théorème d'isomorphisme :

/ 2 U
 

Propriétés de  :

1) ( t,t' ) ² , e^-it = ( e^it )^-1

2) (t) = 1  t  2

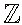
3) (t) = (t')  t - t' 2

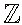
4)  est 2-périodique

5)  est dérivable sur  , t  , ' (t) = ie^it

6) t  , n  , e^int = (e^it)ⁿ ( Formule de Moivre )

Démo du point 5) :

Soient ( t,t' ) ² :

on a :

( e^it' - e^it ) / ( t' - t ) = ( cos t' - cos t ) / ( t'- t ) + i ( sin t' - sin t ) / ( t' - t )

Or lim_t'->t ( cos t' - cos t ) / ( t' - t ) = -sin t

et lim_t'->t ( sin t' - sin t ) / ( t' - t ) = cos t

D'où lim_t'->t ( e^it' - e^it ) / ( t' - t ) = -sin t + icos t = i( cost +isin t ) = ie^it
 
 

III) Etude de la fonction de variable réelle : t e^at , a :
 

Notons  :  , t e^it

Soit a  , on pose a =c + id , ( c , d ) ²

Définition :

t  , e^at = e^{ct + idt}  = e^ct(dt)

Posons :  :  , t  e^at = e^ct( cos dt + isin dt )
 

Rque :

Si d = 0 ,alors a 
 
 

Propriétés :

1)  est dérivable sur  , '(t) = ae^at

2) ( t,t' ) ² , ( t + t' ) = (t)(t')

3)  est un homomorphisme de (  , + ) dans (^* , . )
 

Rque : ( importante )

n'est pas surjective

(on a vu que  était à valeurs dans U ,mais  ne l'est pas car |  | croît )
 
 

V) Applications :

1) Retrouver les formules d'Euler à l'aide de e^z

2) Utilisation des formules d'Euler et de Moivre afin de transformer des produits en sommes , linéarisation . Application de la linéarisation au calcul d'intégrales.

exples :

a) Transformer sin cos ( 2 ) en somme
b) Linéariser cos⁵x
c)  Calcul de I = sin( 2t )cos( 3t )dt

3) En géométrie :

R =  repère orthonormé du plan .

a) L'application g : PP , M (d'affixe z) M' (d'affixe z' ) avec z' = zeⁱ

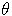
(où  est un argument de z ) est la rotation R(O, )

b) L'application h : PP ,M (d'affixe z ) M' (d'affixe z' ) avec z' = kzeⁱ(où k est réel )

est la similitude S(O,, k)
 
 

4) Calculs de sommes :

A =  cos( kx + (k-1)x )

B =  C_n^k cos ( kx )

C =  (cos(kx) ) / (cos x)^k , x/2 + k , k
 

5) Racines n-ièmes d'un nombre complexe :

6) Résoudre l'equation différentielle suivante :

 

Retour titres des leçons(1)

Retour titres des leçons(2)

Retour page d'accueil Coin des Matheux