Représentation géométrique des nombres complexes.Interprétation géométrique des applications : zz+b , zaz et z ,où a et b ,a0.Exemples d'application à l'étude de configurations géométriques du plan.

Environnement :

• P plan affine euclidien . Repère R
•   espace vectoriel associé . Base (,)

Pré requis :

• Espace affine euclidien ,espace vectoriel,produit scalaire, déterminant avec n =2
• Définition et propriétés algébriques de 
• Mesures d'angles,trigonométrie
• Définition translation,réflexion,similitude.

I) Représentation géométrique d'un complexe :

1) Affixe :

: P , z =x + iyM(x,y) dans R

Résultat :

est bijective

Conséquence :

z ,  ! MP

Déf :

Soit z = x + iy  . M(x,y) est appelé image de z et z est appelé affixe de M.

Notation :

z =  affixe(M) , M(z)

Déf :

On appelle affixe de  , l'affixe du point M vérifiant  = 

Rque :

1) Si aff(M) = z  , M(x,0) dans R

2) Si aff(M) = z  \  , M(0,y)

Propriétés :

1) M(z) , M'(z')

M = M'  aff(M) = aff(M')

2) (z) , '(z')

aff() = aff(')

3) ,'  ,  , '  ,

aff( + '' ) = aff() + 'aff(')

4) M,M'  P , aff(  ) = aff(M') - aff(M)
 
 

2) Module et argument :

Soit M(z)  P ,alors | z | = OM

Démo :

z = a + ib

| z | = 

OM =  = | z |

Rque :

M(z) , M'(z')  P , MM' = | z' - z |
 

Proposition :

Soit M(z)  P \ {0} ,alors arg z =  [2]

Démo :

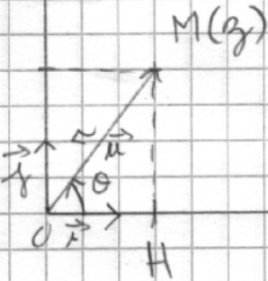
Soit M(z)  P :

r > 0 ,    ] - ;  [ , z = r (cos  + isin  )

M(x,y) dans R avec :

x = r cos  , y = r sin 

arg(z) =  [2] , r = | z |

OH/OM = x/r = cos  et MH/OM = y/r = sin   ( ATTENTION : n'est valable que si M est dans le quadrant de droite)

arg(z) =   [2]
 

Rque :

Le complexe O n'a pas d'argument

Proposition :

M(z) , M'(z')  P \ {0}

(  , ' ) = arg( z'/z ) [2]
 

Démo :

(  , ' ) = (  , ' ) - (  ,  )

= arg(z') - arg(z) [2]

= arg( z'/z ) [2]
 
 

3) Produit scalaire, déterminants :

Proposition :

Soient (z) , '(z')  , alors :

1)  . ' = Re( z )

2) det(,' ) = -Im(z)
 

II) Interprétation géométrique de z z + b , z az , z ( a,b ,a  0 ) :

1) f₁ : z z + b

₁ : P P , M(z)  M'(z') , z' = z + b
 

Proposition :

₁ est la translation de vecteur (b)

Démo :

aff() = aff(M') - aff(M)

           = z' - z = z + b - z = b = aff( )

D'où  = 
 

2) f₂ : z az

₂ : P P , M(z)  M'(z') , z' = az
 

Proposition :

1) Si a = 1 , ₂ est l'identité de P

2) Si a  1 , ₂ est la similitude de centre O ,de rapport | a | ,d'angle une détermination de arg(a)
 

{ z  / f₂(z) = z }

f₂(z) = z  az = z  (a-1)z = 0 (E)

• Si a = 1 ,(E) est satisfaite quel que soit z complexe

alors f₂ = Id , ₂ = Id_P

• Si a  1 :

(E)  z = 0

O est le seul point invariant par ₂

OM' = | z' | = | az | = | a | | z | = | a | OM

( , ' ) = arg( z'/z ) [2] = arg(a) [2]
 

₂ = Sim( O, | a | ,  ) ,  = arg(a) [2]
 

Rque :

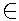
1) Si a   \ {0} , ₂ = hom(O , | a | )

2) Si | a | = 1 , ₂ = rot(O,) ,  =arg(a) [2]
 
 

3) f₃ : z  , ₃ : P P , M(z) M'(z') , z' = 

Proposition :

 ₃ est la reflexion d'axe (x'Ox)

Démo :

z = x + iy , M(x,y) dans R

z' =  = x - iy , M'(x,-y) dans R

₃  est bien la reflexion d'axe (x'Ox)
 

III) Applications :

1) Dans P , muni d'un repère orthonormal 

A(2+2i ) , B(2-2i) , C(-1 +i)

Montrer que (CA)  (CB)
 

2) A₁(z₁), ... , A_n(z_n) ,   ₁ , ... , _n / ₁ + ... + _n   0

G = bar { ( A₁;₁ ) , ... , ( A_n;_n ) }
Donner l'affixe de G
 

3) C1 , C2 et C3 ,3 cercles de même rayon R ,concourant en O.
On note A,B et C ,les 3 autres points d'intersection.
Montrer que le cercle passant par A,B et C est de rayon R.
 

4) On prend un quadrilatère ABCD. On trace des triangles isocèles rectangles extérieurs.

Montrons que :

UW = TV et UW  TV