Utilisation d'arbres,de tableaux,de diagrammes pour des exemples simples de dénombrement.Dénombrement des arrangements et des permutations.
Pré Requis :
I) Représentation graphique :
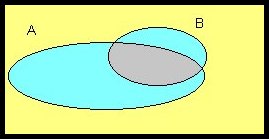
Card(A ![]() B) = Card A +Card B - Card(A
B) = Card A +Card B - Card(A ![]() B)
B)
 Card (
Card (![]() )
= Card E - Card A
)
= Card E - Card A
Exple de dénombrement :
Elèves pratiquant plusieurs langues. (classique)
2) Arbres :
Un arbre représente un ensemble fini d'événements; on le note A.
On le munit d'une relation d'ordre partiel notée"---" vérifiant :
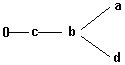
Définitions :
Dans une urne, on dispose de boules blanches et de boules noires.
On effectue des tirages successifs dans cette urne :
Dénombrer les cas possibles. (faire un arbre)
Principe multiplicatif :
Définition :
A est dit régulier de rang m ( supérieur
ou égal à 1 ), si ![]() k
k ![]() [|
0,m-1 |] au rang k,chaque ramification a un même nombre de branches.
[|
0,m-1 |] au rang k,chaque ramification a un même nombre de branches.
Théorème :
Soit A régulier de rang m ( supérieur ou égal à 1 );
Soit (nk)0![]() k
k![]() m
- 1
m
- 1
nk le nombre de branches de la kième
ramification, alors A a ![]() éléments terminaux.
éléments terminaux.
Preuve : par récurrence sur le rang de A
II) Arrangements ,permutations :
Soit n > 0 , n![]() p >0 :
p >0 :
E= { x1,x2,…,xn } ,ensemble à n éléments distincts.
Déf:
Un p-arrangement de E est un p-uplet d'éléments distincts de E.
Théorème :
Le nombre de p-arrangement de E est n(n-1)…(n-p+1).
On le note ![]()
Une permutation de E est un n-arrangement de E.
Théorème :
Il y a n(n-1)…2*1 permutations. On note ce nombre : n !
Rque :
Pour o![]() p < n ,
p < n ,![]() =
=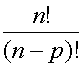
Pour p=n on pose 0! =1 , Ann
= ![]() = n!
= n!
III) Exples d'utilisation :