I) Combinaisons :

1) Définition :

Soit E un ensemble fini de cardinal n ( n * )
E ={ x₁,...x_n } et un entier p ;

On appelle combinaison de p éléments parmi n toute partie de E possédant p éléments.
 

Un tirage du loto est une combinaison de 6 éléments parmi 49 qui appartiennent à { 1,...,49 }.
 

 2) Dénombrement des combinaisons :

L'ensemble des parties à p éléments de E est inclus dans P(E), donc fini.
On note alors  le nombre de combinaisons de E à p éléments de E .
 

Remarque : Quand p>n,  = 0

Théorème :

  =

Dém :

* Si p=0 il n'y a qu'une seule partie contenant 0 élément : 

Si p=0,alors   = 1 (par convention 0! =1)

* Si 1pn :

= { p-arrangements de E }
Soit { x_i1,...,x_ip} une partie à p éléments de E.
A_{{ xi1,...xip }} = { p-arrangements qui contiennent x_i1,...,x_ip }
                    = { (f(x_i1)),...,(f(x_ip)), f bijection sur { x_i1,...,x_ip} }

⁼_{{ xi1,...,xip } E} A_{{ xi1,...xip }}
 
 

Card = Card { parties à p éléments }* Card A_{{ xi1,...xip }}

_D'où

= _* p!

Donc :

=

Exple :

Il y a C⁶₄₉= 1 398 816 tirages de loto différents.
 

3) Propriétés :

i) C⁰_n = 1 , C¹_n = n , Cⁿ_n = 1
ii)  = 
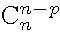
iii) n2  =  +  avec 1pn-1
 

Soit a  E.
P_p(E) = { parties à p éléments de E }

E₁ = { parties à p éléments qui contiennent a }
E₂ = { parties à p éléments qui ne contiennent pas a }

P_p(E) = E₁E₂ , E₁E₂ = 

* f : E₁{ parties à p-1 éléments de E \ {a} }
     { x_i1,...,x_ip-1,a } { x_i1,...,x_ip-1 }

f bijective.Donc Card E₁ = 

* g : E₂{ parties à p éléments de E \ {a} }
     { x_i1,...,x_ip }{ x_i1,...,x_ip }

Card E₂ = 

D'où le résultat .
 

Exercice :( Van der Monde )

( a,b,p )³     0pa+b ,alors on a :

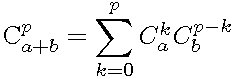
Conséquence :

Si a=b=p   ,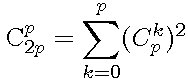

II) Formule du binôme :

Théorème :

( a,b )² , n 

( a+b )ⁿ =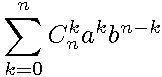 

Démo: Par récurrence sur n (utiliser la formule  =  +  )
 
 

III) Applications :

1) Dénombrement :

binôme a=b=1
(1+1)ⁿ = 2ⁿ = C⁰_n + C¹_n+ ... +Cⁿ_n

_{Dans P(E) :}

• il y a C⁰_n parties à 0 élément
• il y a C¹_n parties à 1 élément

...

• il y a Cⁿ_n parties à n éléments

Card P(E) = C⁰_n + C¹_n+ ... +Cⁿ_n = 2ⁿ

^{2) Trigonométrie :}

^{Linéarisation}

^{3) Arithmétique :}

Petit théorème de Fermat : a  , p premier ,alors a^pa[p]

(* indication : Utiliser le lemme suivant : si p premier,alors :
0<k<p , p | C^k_p . Ensuite,pour prouver Fermat, faire un récurrence sur a )

4) Analyse : formule de Leibniz
 
 

Retour titres des leçons(1)

Retour titres des leçons(2)

Retour page d'accueil Coin des Matheux