Première partie : Question de cours
 

Soient E et F deux espaces vectoriels sur un corps K ,et soit  un élément de (E,F), c'est-à-dire une application linéaire de E vers F ; démontrer les résultats de cours suivants :
 

1) Proposition : (0_E) = 0_F

2) Théorème :  est injective si et seulement si Ker  = {0_E}

3) Théorème : Si  est bijective alors ^-1 (F,E)

Deuxième partie : Exercices

Exercice 1 :

Résoudre dans  , l'équation : z² - (5 + 8i)z + (13 + 35i ) = 0

( Indication 11881^0.5 = 109 )

Détailler soigneusement les calculs ,et expliciter clairement les solutions.
 

Exercice 2 :

Soit f une application de  dans  ,et soit la proposition suivante :

> 0 , M > 0 ,  x  , ( | x | > M et | f(x) |  )

a) Nier cette proposition
b) "Simplifier" cette négation en faisant apparaître ""
 

Exercice 3 :

Parmi les sous-ensembles suivants de ³ ,déterminer lesquels sont des sous-espaces vectoriels .

(i) F_i = {(a,b,c) / a + 2c = 5b }
(ii) F_ii = {(a,b,c) / 2a + 3b = 1 }
(iii) F_iii = {(a,b,c) / a² + b² = 0 }
(iv) F_iv = {(a,b,c) / a² + c² = 2ac }
 

Exercice 4 :

Soit dans ⁴ :

F = {(x,y,z,t) ⁴ / x + y + z + t = 0 } et G ={ (,,,) /   }

1) Montrer que F et G sont des sous-espaces vectoriels de ⁴
2) Montrer que F et G sont supplémentaires
3) Soit v⁴  , déterminer l'unique couple(f,g)  FG tel que :
v = f + g

Exercice 5 :

Soit f(⁴ ; ³ ) définie par :

f : ^4  3 , (x,y,z,t)  ( x + 5y + 2z + t, 3x + 14y + 10z + 7t, 2x + 13y -8z - 10t )

Soit  et  les bases canoniques respectives de ⁴ et ³ .

( c'est-à-dire :  = ( (1,0,0,0),(0,1,0,0),(0,0,1,0),(0,0,0,1) )
et  = ( (1,0,0),(0,1,0),(0,0,1) )        )
 

1) Donner la matrice M de f par rapport aux bases  et  .
(M = Mat(f,,) )

2) Déterminer Ker f en en donnant les équations cartésiennes (on exprimera les premières composantes x et y en fonction des dernières z et t ) et une base .

3) Déterminer Im f en en donnant les équations cartésiennes et une base .

4) Ker f et Im f sont-ils supplémentaires ?

On considère maintenant dans ³
la base ' = ( (1,1,1),(1,-2,1),(1,0,-1) )

5) a) Déterminer P = Mat(Id³  ,', )
  b) Déterminer Q = Mat(Id³ ,  ,' )
  c) Déterminer N = Mat(f, ,' )
 

Exercice 6 :

Soient E et F deux espaces vectoriels sur un corps K, et soit (E,F)
On définit la relation  sur E par :

1) Montrer que  est une relation d'équivalence sur E

2) Soit x  E ,déterminer Cl(x) que l'on notera plus simplement 

3) On note E / Ker  l'ensemble quotient E / ; on munit cet ensemble d'une loi de composition interne "+" et d'une loi de composition externe "." par :

x,y  E ,  +  =  et x  E ,  K, . = 

Montrer que ces deux lois sont bien définies, c'est-à-dire que :

a) x,x',y,y'  E , si  = ' et  = ' alors  = 

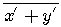
b) x,x'  E ,  K si  = '  alors  = '
 

4) Montrer soigneusement que E / Ker  muni de ces deux lois possède alors une structure d'espace vectoriel sur K .

( Attention : E / Ker  n'est pas un sous-espace vectoriel de E car E / Ker  n'est pas inclus dans E )

5) On définit maintenant l'application  de E / Ker  dans Im  par :

: E / Ker   Im  , (x)

a) Montrer que  est bien définie (c'est-à-dire que () ne dépend pas du représentant choisi (ici x) de la classe  ) .

b) Montrer que  est linéaire.

c) Montrer que  est bijective.